Probability with fractions quiz
Probability with fractions quiz, Test your skills through this exercise
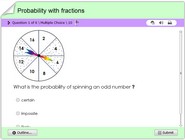
Finding the probability with notions of fractions, math quiz online
The probability of something happening or not is is common in daily life phenomena. We often talk to the likelihood or unlikelihood of something happening. For example if you spin the wheel what will happen etc. The notion of fractions is also part of this concept and in this interactive math online quiz children will solve problems that involve probability. This is a multiple choice test and it is a great way for kids to get extra practice at home or in the classroom. This quiz is also in line with common core state standards for 5th, 6th and 7th grades.
Probability is a measure of the likelihood of an event occurring. It is expressed as a fraction, with the numerator representing the number of successful outcomes and the denominator representing the total number of possible outcomes. For example, if you were flipping a coin, the probability of getting heads would be 1/2, since there are two possible outcomes (heads or tails) and only one of them is a successful outcome (getting heads).
Probability can also be expressed as a percentage. To convert a probability from fraction form to percentage form, simply multiply the fraction by 100%. For example, the probability of getting heads when flipping a coin is 1/2, or 50% in percentage form.
There are several rules that hold true for probability. The first is that the probability of an event occurring is always between 0 and 1 (or 0% and 100% in percentage form). An event with a probability of 0 means that it is impossible for the event to occur, while an event with a probability of 1 (or 100%) means that it is certain to occur.
The second rule is the sum rule, which states that the probability of all possible outcomes occurring is always equal to 1 (or 100%). For example, the probability of flipping heads or tails when flipping a coin is 1, since both outcomes are possible.
The third rule is the multiplication rule, which states that the probability of two events occurring is equal to the probability of the first event occurring multiplied by the probability of the second event occurring. For example, if you have a bag with 5 red balls and 5 blue balls, and you draw one ball out of the bag without replacing it, the probability of drawing a red ball and then a blue ball would be (5/10) * (4/9) = 2/9.
Probability can be used to make predictions about the likelihood of an event occurring. For example, if you know that it rains on 20% of the days in a particular month, you can use this information to predict the probability of it raining on a given day in that month.
Probability can also be used to make decisions. For example, if you are deciding whether or not to buy a lottery ticket, you might consider the probability of winning the lottery as part of your decision-making process.
There are many different types of probability, including classical probability, empirical probability, and subjective probability. Classical probability is based on the idea that all outcomes are equally likely to occur, while empirical probability is based on observations of events that have already occurred. Subjective probability is based on an individual’s personal belief about the likelihood of an event occurring.
Probability theory is a branch of mathematics that deals with the study of probability. It has many applications in fields such as finance, insurance, and statistics. Probability is a fundamental concept in mathematics and has many practical applications in real-world situations.