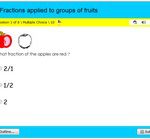
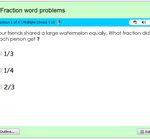
Fractions applied to groups of animals quiz
Practice Fractions with applied to groups of animals math quiz.
Learn how to match fractions with pictures
Fractions are a common topic in mathematics, and understanding how to work with them is an important skill for students to learn. Fractions represent a part of a whole, and they can be written in a variety of ways. For example, the fraction 1/2 represents one half of a whole, while 3/4 represents three quarters of a whole. In this article, we will take a closer look at fractions, including how to write them, how to compare them, and how to perform basic operations with them.
One way to represent a fraction is with a simple fraction, also known as a common fraction. A simple fraction is written as a ratio of two integers, with the numerator (the top number) representing the part and the denominator (the bottom number) representing the whole. For example, the fraction 1/2 represents one half of a whole, while 3/4 represents three quarters of a whole.
Another way to represent a fraction is with a mixed number. A mixed number consists of a whole number and a fraction. For example, the mixed number 1 1/2 represents one and a half. To convert a mixed number to a simple fraction, you can rewrite the mixed number as an improper fraction. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, to convert 1 1/2 to a simple fraction, we can rewrite it as 3/2.
There are several ways to compare fractions. One way is to compare the numerators of the fractions, which tells us which fraction has a larger part. For example, in the fractions 3/4 and 1/2, the numerator of 3/4 is larger, so 3/4 has a larger part. Another way to compare fractions is to compare the denominators of the fractions, which tells us which fraction represents a smaller part of the whole. For example, in the fractions 3/4 and 1/2, the denominator of 1/2 is smaller, so 1/2 represents a smaller part of the whole.
To perform basic operations with fractions, it is important to first make sure that the fractions have the same denominator. This is known as finding a common denominator. For example, to add the fractions 1/2 and 3/4, we need to find a common denominator. One way to do this is to find the least common multiple of the denominators, which in this case is 4. We can then rewrite the fractions as 2/4 and 3/4, which have the same denominator of 4. We can then add the fractions by adding the numerators and keeping the same denominator: 2/4 + 3/4 = 5/4.
We can also perform other basic operations with fractions, such as subtraction, multiplication, and division. For example, to subtract the fractions 3/4 and 1/2, we can again find a common denominator of 4 and rewrite the fractions as 3/4 and 2/4. We can then subtract the fractions by subtracting the numerators and keeping the same denominator: 3/4 – 2/4 = 1/4. To multiply fractions, we can simply multiply the numerators and denominators: 1/2 x 3/4 = 3/8. To divide fractions, we can invert the second fraction and then multiply the fractions: 1/2 ÷ 3/4 = 1/2 x 4/3 = 4/6 = 2/3.
In conclusion, fractions are an important concept in mathematics that allow us to represent a part of a whole. There are several ways to represent fractions, including simple fractions and mixed numbers, and there are several ways to compare them.