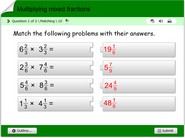
Multiplication of fractions with whole numbers quiz
Learn how to do multiplication of fractions with whole numbers quiz?
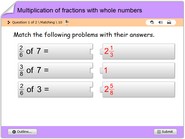
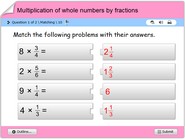
How to multiply fractions with whole numbers?
Multiplying fractions with whole numbers can be a bit tricky, but once you understand the concept, it’s not that hard. A fraction is a way of representing part of a whole, with the top number being the numerator and the bottom number being the denominator. A whole number is a number that is not a fraction, like 1, 2, 3, and so on.
When we multiply a fraction by a whole number, it’s important to remember that we are multiplying the numerator by the whole number and the denominator stays the same. Let’s look at an example:
3 x (2/3) = 6/3
In this example, we are multiplying the whole number 3 by the fraction 2/3. We multiply 3 by the numerator, 2, and get 6. The denominator stays the same, so the answer is 6/3.
Another example is 2 x (5/4) = 10/4
It’s important to remember that the denominator stays the same while the numerator is multiplied by the whole number.
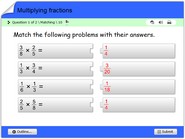
We can also multiply a whole number by a mixed number (whole number and fraction). Let’s look at an example of that:
3 x 2 1/2 = 7 1/2
In this example, we are multiplying the whole number 3 by the mixed number 2 1/2. To do this, we first need to convert the mixed number to an improper fraction. So, 2 1/2 is converted to (22)+1/2 = 5/2. Now we can multiply 35/2 = 15/2 = 7 1/2 which is our final answer.
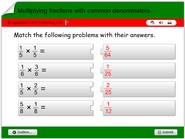
It’s also important to note that when we multiply fractions by whole numbers the product is always in the form of mixed number or whole number.
It is also important to note that when solving multiplication problems of fractions and whole numbers, it’s important to clearly understand the problem statement and simplify the fraction when you can.
Practice and understanding the rules of fractions and the numerator and denominator would be very helpful in solving multiplication problems of fractions and whole numbers.
Another way to think about it is that if you have 4 apples and you have 1/2 of an apple, you can multiply 4*1/2 which is 2 apples. So in this example 4 is the whole number and 1/2 is the fraction.