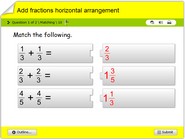
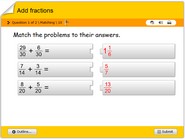
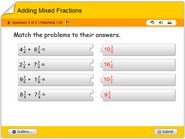
Add fractions horizontal arrangement quiz
Learn to add fractions in a horizontal arrangement, math quiz online.
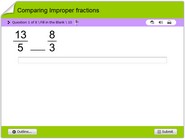
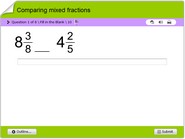
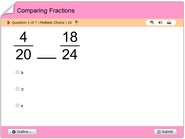
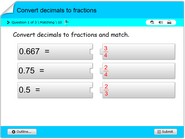
Addition of fractions math test online for children
Addition of fractions math test online for children in 3rd to 7th grades. To successfully take this quiz, children must understand notions of finding the LCM of two numbers. They also have to understand the rules needed in adding fractions. This quiz will improve mental math abilities of children. It will also enable them to self-evaluate their math skills and improve on areas of weakness. This quiz is multiple choice math trivia online and there is no limit as to how many times it could be taken.
When we add fractions, we are finding the total amount when we combine two or more parts together. Imagine you have a pizza and you want to divide it into 4 equal slices. Each slice would be one fourth of the pizza, or 1/4. If you had two slices, the total amount of pizza you would have would be 2/4, which is the same as 1/2. This is because when you add the two parts together (2/4), you are finding the whole (1/2).
When adding fractions, it is important to make sure that the fractions have the same denominator, or bottom number. This is because the denominator tells us how many parts the whole is divided into. If the denominators are different, it can be difficult to add the fractions because they are not talking about the same number of parts.
For example, if you wanted to add 1/4 and 1/3 together, you would need to first find a common denominator. A common denominator is a number that both fractions can be converted to, so that they have the same denominator. In this case, a common denominator would be 12 because 4 and 12 have no common factors other than 1 and 3 and 12 are the least common multiple.
Now that we have a common denominator, we can convert 1/4 to 3/12 and 1/3 to 4/12. Now we can add these fractions, 3/12 + 4/12 = 7/12
It is also possible to add fractions that are arranged horizontally, which means the fractions are lined up next to each other. When adding fractions in this way, it is important to remember that the denominators, or bottom numbers, must still be the same.
For example, if you wanted to add 2/5, 3/5 and 1/5 together, you would line them up horizontally and add the numerators, or top numbers, together:
2/5 + 3/5 + 1/5 = 6/5
It is important to notice in this case, the result of this sum is a mixed number. 6/5 is the same as 1 1/5, which is the same as 6/5.
It’s very important to note that when working with fractions, it is important to simplify the fractions to lowest terms whenever possible.
In general, when adding fractions, you can think of it as combining parts of a whole. The denominators tell us how many parts the whole is divided into, and the numerators tell us how many of those parts we have. By adding the numerators together and keeping the denominator the same, we can find the total amount when we combine the parts together.
In summary, when adding fractions, it’s necessary to have the denominators the same and add the numerators together. In case the denominators are not the same, it’s required to find a common denominator first. Also, it’s always a good idea to simplify the fractions to lowest terms whenever possible.