Quizzes 1 | Math Fractions Activities for Children in 2nd, 3rd, 4th, 5th, 6th and 7th Grades, Games, Quizzes, Worksheets

Circle graphs quiz

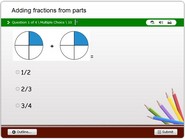
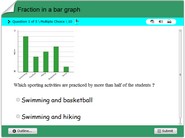
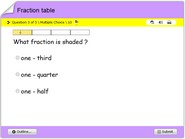
Circle graphs, data & fractions math quiz online for kids.

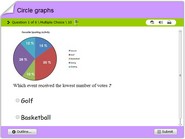
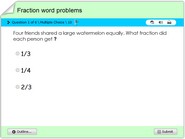
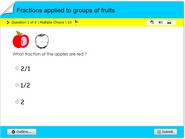
Math quiz online on proportions of circle graphs

Math quiz online on proportions of circle graphs. In this math quiz, children will understand how data is represented on circle graphs also referred to as pie charts. These graphs have several fraction proportions represented with varying colors. Each problem contains a multiple choice answer option such that after solving a problem, children could find corresponding answers. This game also imparts the notion of fractions of a circle, integrated to representing data proportionately. This also works as a game, test or quiz for children in 3rd, 4th, 5th, 6th or 7th grades. Have fun online with this interactive activity.

A circle graph, also known as a pie chart, is a graphical representation of data that displays the proportions of different parts of a whole. It is a circular chart divided into sectors, with each sector representing a proportion of the total. Circle graphs are often used to compare the parts of a whole and to illustrate the relationships between the different parts.

To create a circle graph, you first need to determine the total value of the data being represented. Then, each value is represented as a percentage of the total, and this percentage is used to determine the size of the corresponding sector in the circle graph. The sectors are then arranged around the circle in a clockwise direction, with the largest sector at the top.

There are several considerations to keep in mind when creating a circle graph. First, the data should be organized into categories that are mutually exclusive and exhaustive, meaning that each data point belongs to only one category and all data points are accounted for. This ensures that the sum of the parts equals the whole.

Second, the number of categories should be limited to no more than six or seven, as a circle graph with too many categories can be difficult to interpret. If the data has more than six or seven categories, it may be more effective to use a different type of graph, such as a bar graph or a stacked bar graph.

Third, the sectors should be labeled with both the category name and the value of the data. This allows the reader to easily understand the meaning of each sector. It is also important to include a key or legend to explain the meaning of each color or pattern used in the circle graph.

Circle graphs can be useful for visualizing data and comparing the proportions of different parts of a whole. However, they are not suitable for showing changes over time or for illustrating detailed data. In these cases, a different type of graph, such as a line graph or a bar graph, may be more appropriate.

Quizzes that involve circle graphs may ask questions about the interpretation of the data represented in the graph, the relationship between the different parts of the whole, or the comparison of the proportions of different categories. They may also include questions about the construction of a circle graph, such as how to determine the size of the sectors or how to label the graph.

To succeed on a quiz that involves circle graphs, it is important to understand the basics of how these graphs are constructed and interpreted. It is also helpful to be familiar with the strengths and limitations of circle graphs, as well as the appropriate situations in which they should be used.

$Adding-fractions-from-parts$

Adding fractions from parts quiz

Adding fractions from parts math quiz for practice and testing your skills.

Illustrated math exercise on adding parts of fractions

Illustrated math exercise on adding parts of fractions. In this exercise, children will learn how to add portions of a shape to arrive at sums of other fractions. This is a multiple choice test questions and a trivia math quiz for children in 2nd, 3rd, 4th and 5th grades. It could serve as a math test online or a review activity at home. Each problem contains a graphic showing two fraction values shaded on a circle or any other geometric shape. Takers of the quiz have to find out the sum of both fractions with the aid of each given picture. This game also serves as an interactive online math multiple choice question test.

Adding fractions with the same denominator is a straightforward process. The sum of the fractions is equal to the sum of the numerators, with the denominator remaining the same. For example, if we have the fractions 1/2 and 1/2, we can find the sum by adding the numerators together to get 2/2, or simply 1.

However, things can get a bit more complicated when the fractions have different denominators. In this case, we need to first find a common denominator before we can add the fractions. A common denominator is a number that is a multiple of both of the fractions’ denominators.

For example, consider the fractions 1/2 and 1/3. To add these fractions, we need to find a common denominator that is a multiple of both 2 and 3. The least common multiple of 2 and 3 is 6, so we can use 6 as the common denominator.

To express 1/2 and 1/3 with a denominator of 6, we need to rewrite them as fractions with 6 as the denominator. To do this, we use the following formula:

New fraction = (numerator x common denominator) / original denominator

Using this formula, we can rewrite 1/2 as follows:

New fraction = (1 x 6) / 2 = 3/6

We can do the same thing with 1/3 to get a new fraction of 2/6.

Now that both fractions have a common denominator of 6, we can add them together by simply adding the numerators. The sum of 3/6 and 2/6 is 5/6.

Another way to add fractions with different denominators is to use the least common multiple (LCM) of the denominators as the common denominator. The LCM is the smallest number that is a multiple of both denominators. In the example above, the LCM of 2 and 3 is 6, so we could also use the LCM method to find the common denominator.

It’s important to note that the LCM is not always the same as the common denominator. For example, the fractions 1/4 and 1/6 have a common denominator of 12, but the LCM of 4 and 6 is 12. In this case, using the LCM as the common denominator would work, but it’s not always the case.

Once you have found the common denominator, the process of adding the fractions is the same as if the fractions had the same denominator. Simply add the numerators and write the sum as a fraction with the common denominator.

In summary, to add fractions with different denominators:

Find a common denominator, either by using a multiple of both denominators or the least common multiple of the denominators.
Rewrite each fraction with the common denominator using the formula: (numerator x common denominator) / original denominator.
Add the numerators of the new fractions to find the sum.

Fraction in a bar graph quiz

Test your fraction knowledge with this fraction in a bar graph quiz exercise.

Bar graphs and fractions math quiz online for children

Bar graphs and fractions math quiz online for children to review. Representing data on bar graphs some times warrants that children to understand the notion of fractions. This free math online test contains a number of math problems containing a bar graph from which children have to estimate what fraction of the data represents a particular entity as required by each question. This is a multiple choice questions test and children have the flexibility to make several attempts. By doing this activity repetitively, the notion representing data visually as well as data interpretation will be passed along. This quiz will work for children in 3rd, 4th, 5th, 6th and 7th grades.

A bar graph is a visual representation of data, using bars of different lengths to show the quantities or proportions of the data. Fractions can be used on a bar graph to show the part of a whole that each data point represents.

To create a bar graph using fractions, first decide on the data you want to represent. For example, you might want to show the fraction of each type of fruit in a basket of mixed fruit. In this case, you would have one bar for each type of fruit.

Next, decide on a scale for the bar graph. This will depend on the size of the fractions you are working with and the space available on the graph. For example, if you are working with fractions that are all less than 1/2, you might choose a scale of 1/2, 1/4, 1/8, etc. On the other hand, if you are working with larger fractions, you might need to use a larger scale.

Once you have determined the scale for the graph, you can start creating the bars. To create a bar for a fraction, you will need to decide on the length of the bar and the starting point. The length of the bar should be proportional to the size of the fraction, using the scale you have chosen. For example, if the fraction is 1/4 and the scale is 1/4, the bar should be as long as one of the divisions on the scale. If the fraction is 1/2 and the scale is 1/4, the bar should be twice as long as one of the divisions on the scale.

The starting point for the bar will depend on the fractions that came before it. For example, if the fraction is 1/4 and the previous fraction was 1/4, the bar for the new fraction should start at the end of the previous bar. If the previous fraction was 1/2, the bar for the new fraction should start halfway between the end of the previous bar and the beginning of the next division on the scale.

When creating a bar graph with fractions, it’s important to label both the scale and the bars. The scale should be labeled with the fractions that correspond to each division, while the bars should be labeled with the data they represent. For example, in the fruit basket example, the bars might be labeled “apples,” “oranges,” “bananas,” etc., while the scale might be labeled with fractions such as 1/4, 1/2, 3/4, etc.

It’s also important to include a key or legend on the bar graph to explain what each bar represents. This can be especially useful if the data points are represented by different colors or patterns on the graph.

In addition to showing the data as fractions, you can also use a bar graph to compare fractions. For example, you might want to compare the fractions of different types of fruit in two different baskets of mixed fruit. To do this, you can create two bar graphs side by side, with one graph for each basket. You can then compare the lengths of the bars on each graph to see which basket has more of a particular type of fruit.

Bar graphs are a useful tool for visualizing and comparing data, and using fractions on a bar graph can help you better understand the proportions of the data. Whether you are working with fractions that represent parts of a whole or fractions that are being compared to each other, a bar graph can be a helpful tool for understanding and interpreting the data.

Fraction table quiz

Fraction table math quiz online, Learn about fractions with this easy exercise.

Find the value of shaded portions on a fraction table, math quiz

Find the value of shaded portions on a fraction table. Math quiz online for children to review their skills online. This is an interactive online math quiz to practice how to use fraction tables. Each problem is a multiple choice questions trivia containing a picture of a section of the table in which a portion has been shaded. Children have to use this guide to find the fraction value from the picture. in case you want to get more offline practice, fractions4kids offers worksheets on this topic which can be used for written tests. Improve you mental math skills and your ability to solve much complex math problems.

Fraction tables can be a helpful tool for students who are learning about fractions, as they allow for quick reference and practice of basic fraction operations. A fraction table quiz can be a fun and effective way for students to test their knowledge of fractions and improve their skills.

To create a fraction table quiz, start by selecting a range of fractions to include. It can be helpful to choose a range of simple fractions, such as halves, thirds, and quarters, as well as more complex fractions. Consider also including mixed numbers and improper fractions in the quiz.

Next, create a table with rows and columns for each fraction. The columns should represent the fractions being multiplied or divided, and the rows should represent the fractions being added or subtracted. For example, a fraction table quiz might include the following fractions: 1/2, 1/3, 1/4, 1/5, 2/3, 3/4, and 4/5.

To create the quiz questions, fill in the fraction table with the results of each operation. For example, if the question is “What is 1/2 + 1/3?”, the answer would be 5/6, which would be placed in the cell where the 1/2 row and 1/3 column intersect.

To make the quiz more challenging, consider including a mix of operations and multiple steps in a single question. For example, a question might be “What is 1/2 * 1/4 + 3/4 / 3/5?” The answer to this question would be 11/20, which would be calculated by first multiplying 1/2 * 1/4 to get 1/8, and then adding 3/4 / 3/5 to get 11/20.

To grade the quiz, provide a key with the correct answers for each question. Students can then compare their answers to the key to see how they did.

In addition to testing students’ knowledge of fractions, a fraction table quiz can also help them practice mental math skills and improve their ability to work with fractions. It can be helpful to review the quiz with students, discussing any questions they had difficulty with and going over the steps for solving them.

Overall, a fraction table quiz is a useful and engaging way for students to learn about and practice working with fractions. By providing a variety of fractions and operations, and including a mix of simple and complex questions, teachers can create quizzes that are both challenging and rewarding for students. So, this is how a fraction table quiz can be useful for students to improve their skills in fractions.

Fraction word problems quiz

Fraction word problems quiz to practice and test your skills.

Solving fraction word problems math quiz online for kids

Solving fraction word problems math quiz online for kids. This is an interactive multiple choice test questions quiz. Each problem contains answer choices from which kids have to select from. After reading a problem, children have to deduce a formula for finding the required fraction. This activity will work well as a supplementary math activity for children in 4th, 5th, 6th an 7th grades who need extra practice on their abilities to solve word problems involving fractions.

Fraction word problems can be a challenging aspect of learning math for many students, as they require not only a strong understanding of fractions, but also the ability to read and interpret word problems. A fraction word problems quiz can be a helpful tool for students to practice and improve their skills in this area.

To create a fraction word problems quiz, start by selecting a range of word problems to include. It can be helpful to choose problems that cover a variety of concepts, such as comparing fractions, adding and subtracting fractions, and converting between fractions, decimals, and percents. Consider also including word problems that involve mixed numbers and improper fractions.

Next, create the quiz by writing out the word problems and providing space for students to show their work and write their answers. For example, a fraction word problems quiz might include the following problems:

Rachel has 3/4 of a pie and Alex has 1/4 of a pie. How much pie do they have in total?
If a recipe calls for 2/3 cup of sugar and you only have 1/2 cup, how much more sugar do you need to add?
A shirt that was originally $30 is on sale for 25% off. What is the sale price of the shirt?

To make the quiz more challenging, consider including word problems that involve multiple steps or require students to use multiple concepts. For example, a problem might be “On Monday, Alex had 1/4 of a bag of candy. On Tuesday, he ate 3/8 of the remaining candy. On Wednesday, he had 1/4 of the remaining candy left. How much candy did Alex have left on Wednesday?”

To grade the quiz, provide a key with the correct answers and solutions for each problem. Students can then compare their answers and solutions to the key to see how they did.

In addition to testing students’ knowledge of fractions, a fraction word problems quiz can also help them practice their problem-solving skills and improve their ability to read and understand word problems. It can be helpful to review the quiz with students, discussing any problems they had difficulty with and going over the steps for solving them.

Overall, a fraction word problems quiz is a useful and engaging way for students to practice and improve their skills in working with fractions. By providing a variety of problems that cover different concepts and include different levels of difficulty, teachers can create quizzes that are both challenging and rewarding for students. So, this is how a fraction word problems quiz can be useful for students to improve their skills in fractions.

Fractions applied to groups of animals quiz

Practice Fractions with applied to groups of animals math quiz.

Learn how to match fractions with pictures

Fractions are a common topic in mathematics, and understanding how to work with them is an important skill for students to learn. Fractions represent a part of a whole, and they can be written in a variety of ways. For example, the fraction 1/2 represents one half of a whole, while 3/4 represents three quarters of a whole. In this article, we will take a closer look at fractions, including how to write them, how to compare them, and how to perform basic operations with them.

One way to represent a fraction is with a simple fraction, also known as a common fraction. A simple fraction is written as a ratio of two integers, with the numerator (the top number) representing the part and the denominator (the bottom number) representing the whole. For example, the fraction 1/2 represents one half of a whole, while 3/4 represents three quarters of a whole.

Another way to represent a fraction is with a mixed number. A mixed number consists of a whole number and a fraction. For example, the mixed number 1 1/2 represents one and a half. To convert a mixed number to a simple fraction, you can rewrite the mixed number as an improper fraction. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, to convert 1 1/2 to a simple fraction, we can rewrite it as 3/2.

There are several ways to compare fractions. One way is to compare the numerators of the fractions, which tells us which fraction has a larger part. For example, in the fractions 3/4 and 1/2, the numerator of 3/4 is larger, so 3/4 has a larger part. Another way to compare fractions is to compare the denominators of the fractions, which tells us which fraction represents a smaller part of the whole. For example, in the fractions 3/4 and 1/2, the denominator of 1/2 is smaller, so 1/2 represents a smaller part of the whole.

To perform basic operations with fractions, it is important to first make sure that the fractions have the same denominator. This is known as finding a common denominator. For example, to add the fractions 1/2 and 3/4, we need to find a common denominator. One way to do this is to find the least common multiple of the denominators, which in this case is 4. We can then rewrite the fractions as 2/4 and 3/4, which have the same denominator of 4. We can then add the fractions by adding the numerators and keeping the same denominator: 2/4 + 3/4 = 5/4.

We can also perform other basic operations with fractions, such as subtraction, multiplication, and division. For example, to subtract the fractions 3/4 and 1/2, we can again find a common denominator of 4 and rewrite the fractions as 3/4 and 2/4. We can then subtract the fractions by subtracting the numerators and keeping the same denominator: 3/4 – 2/4 = 1/4. To multiply fractions, we can simply multiply the numerators and denominators: 1/2 x 3/4 = 3/8. To divide fractions, we can invert the second fraction and then multiply the fractions: 1/2 ÷ 3/4 = 1/2 x 4/3 = 4/6 = 2/3.

In conclusion, fractions are an important concept in mathematics that allow us to represent a part of a whole. There are several ways to represent fractions, including simple fractions and mixed numbers, and there are several ways to compare them.

Fractions applied to groups of fruits quiz

Math Fractions quiz applied to groups of fruits exercise.

Math quiz on finding fractions that represent a given number of fruits

Math quiz on finding fractions that represent a given number of fruits. This is a free math activity for children in 1st, 2nd and 3rd grades to review their fraction skills. This quiz depending on how you look at it could be considered a math test or a math game online. It is a great way to learn because children get instant feedback as they play along. This quiz is an interactive math activity which uses pictures and visual aids to enable kids catch the notions easily. Have free fun online and please help us to spread the word.

Finding fractions that represent a given number of fruits can be a useful skill to have, whether you’re trying to divide a batch of cookies evenly among your friends or trying to come up with the right amount of fruit to include in a recipe. In this math quiz, we’ll look at some different methods for finding fractions that represent a given number of fruits and practice applying them to a variety of different problems.

One way to represent a given number of fruits using fractions is to use unit fractions. A unit fraction is a fraction whose numerator (the top number) is 1 and whose denominator (the bottom number) is a whole number. For example, 1/2, 1/3, 1/4, 1/5, and so on are all unit fractions.

To use unit fractions to represent a given number of fruits, you first need to determine the number of fruits you have. Let’s say you have 8 apples. To represent this number using unit fractions, you could write:

1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8

This may not be the most practical way to represent the number of apples, but it is a way to do it using unit fractions.

Another way to represent a given number of fruits using fractions is to use mixed numbers. A mixed number is a whole number plus a fraction. For example, 2 1/4 is a mixed number that represents 2 whole fruits plus 1/4 of a fruit.

To use mixed numbers to represent a given number of fruits, you first need to determine the number of whole fruits you have. Let’s say you have 8 apples, just like before. To represent this number using mixed numbers, you could write:

8 1/8

This mixed number represents 8 whole apples plus 1/8 of an apple.

You can also use fractions to represent a given number of fruits by finding the least common denominator (LCD) and adding the fractions together. The LCD is the smallest number that all of the fractions’ denominators will go into evenly.

Let’s say you have 3 apples and 2 pears. You could represent this number of fruits using fractions by writing:

3/5 + 2/5

The LCD of 5 is 5, so you don’t need to do any further work to add these fractions together.

Alternatively, you could find the LCD by multiplying the denominators together:

3/5 + 2/5 = (3/5) x (2/2) + (2/5) x (5/5)

= 6/10 + 10/10

= 16/10

This fraction can then be simplified to 1 6/10, which is a mixed number.

You can also represent a given number of fruits using fractions by using equivalent fractions. Equivalent fractions are fractions that have the same value, even though they may have different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions because they both represent the same value (1/2 of a fruit).

To use equivalent fractions to represent a given number of fruits, you can start by finding a fraction that represents the number of fruits you have. Then, you can find equivalent fractions by multiplying or dividing the numerator and denominator by the same number.

Fractions in a group of dots quiz

Fractions in a group of dots quiz Online Practice. Improve your skills with this test.

Finding fraction in group of dots quiz online

Fractions can be a challenging concept for students to understand, but they are an important foundation for more advanced math concepts. One way to help students learn about fractions is through the use of interactive online quizzes, such as a “group of dots” quiz.

In a group of dots quiz, students are presented with a visual representation of a fraction, typically using a group of dots. The dots are divided into two parts, with one part representing the numerator and the other representing the denominator. The student’s task is to identify the fraction represented by the dots.

For example, a student might be shown a group of 8 dots, with 4 of them shaded in. In this case, the student would need to identify the fraction as 4/8, or 1/2.

One of the key benefits of using a group of dots quiz is that it allows students to see the fraction represented visually, rather than just as a written expression. This can help them understand the concept of fractions more intuitively, as they can see the physical division of the dots into two parts.

In addition to identifying fractions, a group of dots quiz may also include questions that require students to compare fractions, order fractions from least to greatest, and add or subtract fractions.

For example, a student might be asked to compare the fractions 3/4 and 5/6. To do this, they would need to understand that the fractions represent different parts of a whole, and then compare the size of the parts to determine which fraction is larger.

To add or subtract fractions, students must first make sure that the fractions have the same denominator. If the denominators are different, the student must find a common denominator by finding the least common multiple of the two denominators. Once the fractions have the same denominator, the student can add or subtract the numerators to find the result.

Overall, a group of dots quiz can be a useful tool for helping students learn about fractions. By providing a visual representation of fractions and incorporating questions that require students to use their fraction skills, these quizzes can help students understand and apply this important math concept.

Fractions in a group of shapes quiz

Fractions in a group of shapes quiz Online. Learn fractions with shapes.

Fractions in a group of mathematical shapes interactive quiz online

Fractions in a group of mathematical shapes interactive quiz online. This quiz will be a great way to test children in 1st, 2nd and 3rd grades on their skills in fractions. It takes the form of a multiple choice quiz with different answers to choose from. Children will solve a problem and select the correct answer. This makes this quiz a great self-test for classroom and homeschool use. This game is in line with common core state stands. It can be taken for free and repetitively.

Learning fractions can be a challenging concept for many students, but teaching fractions using shapes can be a helpful visual aid. Using shapes to teach fractions allows students to see the concept in a concrete way, which can make the abstract concept of fractions more accessible.

One way to introduce fractions using shapes is to begin with a whole shape, such as a circle or square. You can then divide the shape into equal parts, labeling each part as a fraction. For example, if you divide a circle into halves, you can label each half as 1/2. If you divide the same circle into quarters, you can label each quarter as 1/4.

Another way to teach fractions using shapes is to have students create their own fractions using manipulatives, such as pattern blocks or geoboards. For example, a student could use pattern blocks to create a rectangle and then divide it into halves, labeling each half as 1/2. They could also divide the rectangle into thirds, labeling each third as 1/3.

In addition to using manipulatives, you can also use worksheets or online activities to help students practice identifying and creating fractions. These activities can include identifying the fraction that represents a given part of a shape, as well as creating their own fractions by dividing shapes into equal parts.

It’s also important to introduce students to mixed numbers and improper fractions. A mixed number is a fraction that includes a whole number, such as 3 1/2. An improper fraction is a fraction where the numerator (the top number) is larger than the denominator (the bottom number), such as 7/4. By introducing these concepts, students will have a more complete understanding of fractions and how they work.

One way to help students understand mixed numbers and improper fractions is to use a number line. A number line can show students that fractions are just parts of a whole, and that mixed numbers and improper fractions can be represented as points on a number line.

In addition to using a number line, you can also use real-life examples to help students understand fractions. For example, you can ask students to divide a pizza into equal parts and label each part as a fraction. This can help students see that fractions can be used to represent real-life situations, such as sharing food or other resources.

Overall, using shapes to teach fractions can be an effective way to help students understand this challenging concept. By using manipulative, worksheets, online activities, and real-life examples, students can see the concept of fractions in a concrete way, which can make it easier for them to understand and apply this important math skill.

Fractions in a mixed group of dots quiz

Fractions in a mixed group of dots math online test your knowledge.

Finding fractions in a mixed group quiz online for children

Finding fractions in a mixed group quiz online for children in 1st, 2nd and 3rd grades. In this quiz children will be served with visual aids or pictures of groups of items. From the group they will find what fraction is represented by a particular shape or color. This is an interactive online math trivia questions exercise. It is also a fun game and test which children can use to evaluate their notions of fractions. This cool math exercise will work at home and in the classroom as a supplementary math material.

Finding fractions in a mixed group can be a challenging task, especially if you are working with a large number of items. However, with a little bit of practice and some basic math skills, you can easily find fractions in any mixed group.

One way to find fractions in a mixed group is to first identify the fraction that you are looking for. For example, if you are trying to find a quarter of a group, you will need to identify what a quarter looks like. In this case, a quarter would be one out of four equal parts.

Once you have identified the fraction that you are looking for, you can start counting the items in the mixed group. As you count, try to divide the items into equal parts. If you are looking for a quarter, you will want to divide the items into groups of four. If you are looking for a third, you will want to divide the items into groups of three.

As you divide the items into equal parts, keep track of how many parts you have. If you are looking for a quarter, for example, and you have eight items in your mixed group, you will have two quarters (since 8 / 4 = 2).

If you are having trouble dividing the items into equal parts, you can use a visual aid to help you. For example, you could use a ruler or a piece of string to measure out equal parts. This can be especially helpful if you are working with a large number of items.

Another tip for finding fractions in a mixed group is to practice your mental math skills. The more comfortable you are with basic math operations, the easier it will be for you to find fractions in a mixed group.

Finally, don’t be afraid to ask for help if you are struggling to find fractions in a mixed group. There are many resources available, such as online tutorials and math textbooks, that can help you develop your fraction skills.

In conclusion, finding fractions in a mixed group can be challenging, but with a little bit of practice and the right tools, it is a skill that can be easily mastered. Whether you are a student working on a math assignment or an adult trying to divide a group of items, being able to find fractions is an important skill that can come in handy in a variety of situations.