Comparing-equivalent-fractions

Comparing equivalent fractions quiz

Learn Math Comparing equivalent fractions exercise with online quiz.

 

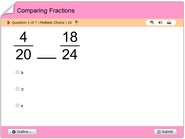
Math quiz on comparing equivalent fractions

Math quiz on comparing equivalent fractions. Children will through this quiz understand how to find numerators and denominators of equivalent fractions. This quiz makes makes the notion of equivalent fractions easy to understand. This activity is a review option for kids in 3rd, 4th, 5th, 6th and 7th grades. Have fun with comparison of equivalent fractions.

When we compare equivalent fractions, we are determining which one is greater or smaller than the other. Equivalent fractions are fractions that have the same value, even though they might have different numerators and denominators.

To compare equivalent fractions, we can start by simplifying the fractions to their lowest form. To simplify a fraction, we find the greatest common factor (GCF) of the numerator and denominator and divide them both by it. For example, 4/8 and 1/2 are equivalent fractions because they are both simplified to 1/2.

Another way to compare equivalent fractions is by cross-multiplying. This method compares the products of the numerators and denominators, instead of just the numerators or denominators.

For example, let’s compare 2/3 and 4/6:

Cross-multiply 2/3 and 4/6, We get (26) and (34) which equals to 12 and 12, therefore the product of the numerator and denominator of the 2 fractions are equal.

We can also compare the fractions by thinking about it as parts of a whole. If we have a whole pizza and want to split it into 8 pieces, we can represent it as 8/8, or 1. Now if we want to split the pizza into 16 pieces instead, we can represent it as 16/16 or 1 as well. Even though they are represented as different fractions, they are both the same, because they both represent the entire pizza.

It’s also important to remember that equivalent fractions can be found by multiplying or dividing both the numerator and denominator by the same number. For example, 2/3 is equivalent to 4/6, because if we multiply both the numerator and denominator of 2/3 by 2, we get 4/6.

In conclusion, comparing equivalent fractions is easy, because they have the same value. We can compare them by simplifying the fractions to their lowest form, cross-multiplying them, or thinking about them as parts of a whole. It’s also important to remember that equivalent fractions can be found by multiplying or dividing both the numerator and denominator by the same number.

Practicing comparing equivalent fractions is a great way to become more familiar and comfortable with this concept. Encourage kids to practice with different fractions and different methods to become confident and comfortable with comparing equivalent fractions.

Convert-decimals-to-fractions

Convert decimals to fractions quiz

In this Practice test we will learn how to Convert decimals to fractions?

Math online quiz on how to convert decimals to fractions

Math online quiz on how to convert decimals to fractions. In this exercise children will have to look at decimal numbers and follow the steps needed to convert them to a fraction. This is a multiple choice question quiz in which kids will solve and match appropriate answers. This math test will also serve as a math game for some kids. At the end of the game players will see their scores displayed. This exercise is suitable for 4th, 5th, 6th and 7th graders.

Converting decimals to fractions can seem like a difficult task for kids, but with the right approach and some practice, it can become a simple and fun concept to understand.

First, it’s important to understand what a decimal is. A decimal is a way of expressing numbers as a combination of whole numbers and parts of a whole. For example, the decimal 0.75 represents the fraction 3/4, because 0.75 can be thought of as three fourths.

When converting a decimal to a fraction, the first step is to write the decimal as a fraction with the decimal number as the numerator (the top number) and the number 1 followed by as many zeros as there are digits to the right of the decimal point as the denominator (the bottom number). For example, to convert 0.75 to a fraction, we would write it as 0.75/1.

Next, simplify the fraction by dividing the numerator and denominator by a common factor. In this example, both the numerator and denominator can be divided by 0.25, resulting in the fraction 3/4.

Another example: 0.5 into fraction: 0.5 = 0.5/1 = (5/10) because any decimal can be written as fraction by putting the number after decimal point as numerator and writing 1 followed by as many zeros as there are digits in denominator = (1/2) because 5 and 10 both can be divided by 5

It’s also possible to convert a decimal that has repeating decimal places, like 0.333…, to a fraction. To do this, you can use a technique called long division.

Here is one way to convert 0.333… to a fraction: Multiply both sides of the equation by a power of 10 that will give you a whole number. So in this case it will be 3 as there are 3 decimal places. 0.333… = 0.333… * 3 = 1

0.333… can now be written as a fraction: 1/3

For kids it’s important to make the topic interactive by using examples from real life which they can relate to. Example: When you divide an pizza into 8 equal slices, each slice is one eight (1/8) of the pizza. If we have 3 slice out of 8 then it will be 3/8 of pizza.

In conclusion, converting decimals to fractions can be a fun and easy concept for kids to understand with the right approach and practice. By using real-life examples, and learning techniques like simplifying fractions, kids can develop a deeper understanding of how decimals and fractions work.

Convert-fractions-to-decimals

Convert fractions to decimals quiz

Math practice through this exercise on how to  convert fractions to decimals.

Math quiz on converting fraction to decimal values

This is a math quiz on converting fraction to decimal values. It is a multiple choice math trivia. The principle is to solve all problems correctly, match them and submit. At the end of the quiz, the score will be displayed and kids can figure out where they went wrong. It is an interesting activity for children in 4th, 5th, 6th and 7th grades. It is also an math game depending on how you look at it. This will work well in school and at home as a supplementary material for studying fractions.

Converting fractions to decimals can seem like a difficult task for kids, but with the right approach and some practice, it can become a simple and fun concept to understand.

First, it’s important to understand what a fraction is. A fraction is a way of expressing a part of a whole. For example, the fraction 3/4 represents three fourths of a whole. The top number, called the numerator, tells you how many parts you have, and the bottom number, called the denominator, tells you how many parts the whole is divided into.

When converting a fraction to a decimal, the first step is to divide the numerator by the denominator. This will give you the decimal representation of the fraction. For example, to convert 3/4 to a decimal, we would divide 3 by 4. Using a calculator or long division, we would get 0.75.

It’s important to make the topic interactive by using examples from real life which they can relate to. Example: Suppose you have 5 pencils out of 8 total pencils, you can express it as 5/8. If you want to know how many pencils are missing, you can subtract 5/8 from 1. and 1-5/8 = 3/8

Similarly you can convert the fraction to decimal, 5/8 = 0.625

For example: When you divide an pizza into 8 equal slices, each slice is one eight (1/8) of the pizza. If you want to know how many slices you have, you can convert the fraction to decimal and say that you have 0.125 slices.

Another way to think about converting fractions to decimals is to think of money. For example, if you have $1 and you want to buy an item that cost $3/4, you can think of the fraction as 75 cents.

In conclusion, converting fractions to decimals and vice versa can be a fun and easy concept for kids to understand with the right approach and practice. By using real-life examples and learning techniques like long division or using calculator, kids can develop a deeper understanding of how fractions and decimals work.

Dividing-fractions

Dividing fractions quiz

Test your skills with this dividing fractions quiz online.

Math test online on how to divide fractions

Review 3rd, 4th, 5th, 6th & 7th grade problems with this math test online on how to divide fractions. In this game children will improve their skills on understanding dividing fraction rules, solving multiple questions in the same area, developing mental math skills etc. This math quiz is also a good math game which could supplement math materials for parents and teachers of kids in primary school. Simple solve a problem, find its corresponding answer, drag and drop.

Dividing fractions is a bit more tricky than adding and subtracting them, but once you understand the concept, it’s not that hard.

First, let’s review what a fraction is. A fraction is a way of representing part of a whole. The top number in a fraction is called the numerator, and the bottom number is called the denominator. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. The fraction 3/4 represents 3 out of 4 equal parts of something.

When we divide fractions, we are trying to find out how many of one fraction will fit into another. For example, if we have 4/5 of a pizza and we want to know how many slices 2/3 of a person will eat, we would divide the fraction of pizza by the fraction of the person. In math terms, this would be written as 4/5 ÷ 2/3.

To divide fractions, we need to do a little bit of flipping and multiplying. The first step is to flip the second fraction (the one being divided into). In our example, we would flip 2/3 to get 3/2.

Next, we will multiply the first fraction by the flipped second fraction. In our example, we would multiply 4/5 by 3/2, which would give us 12/10.

Now we need to simplify the fraction. We know that if we have 10/10 or 20/20, they are equivalent to one whole. So 12/10 is equivalent to 1 and 2/10.

So the final answer to 4/5 ÷ 2/3 is 12/10 = 1 and 2/10.

Another example, 2/3 divided by 4/5 would be (2/3) * (5/4) = 10/12 = 5/6

It is important to remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is found by flipping it. For example, the reciprocal of 4/5 is 5/4.

Dividing fractions may seem tricky at first, but with practice, it can become second nature. If you’re ever stuck, just remember to flip, multiply, and simplify!

In general, when dividing fractions, you invert the divisor (flip the second fraction) and then multiply the fractions, then simplify the result.

It’s also important to note that dividing fractions is not the same as multiplying them by a negative. Dividing by a negative fraction would be the same as multiplying by its reciprocal which is positive.

Also practice and understanding the rules of fractions and the numerator and denominator would be very helpful in solving dividing fraction problems.

Division-of-fractions-by-whole-numbers

Division of fractions by whole numbers quiz

Learn Math with this division of fractions by whole numbers quiz practice online.

Math quiz online for kids to test how to divide fractions by whole numbers

This is a math quiz online for kids to test how to divide fractions by whole numbers. Here children will learn the rules of dividing fractions. This math test is suitable for 4th, 5th, 6th, 7th grade children. It takes the form of an interactive online math quiz with multiple choice questions from which kids can select correct answers. This could also be perceived as a cool math game which will keep kids excited in a classroom or at home.

Dividing fractions by whole numbers can be a bit tricky, but it’s an important skill to learn because it will help you solve a lot of math problems.

Let’s start by reviewing what a fraction is. A fraction is a way to represent a part of a whole. The top number of a fraction is called the numerator, and the bottom number is called the denominator. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4.

When we divide a fraction by a whole number, we are basically asking “How many times does the whole number fit into the fraction?” To do this, we flip the whole number and turn it into a fraction with a numerator of 1. This is called the reciprocal of the whole number.

Let’s take an example:

Suppose we have the fraction 2/3 and we want to divide it by the whole number 2. To do this, we flip 2 to get 1/2, and then we multiply 2/3 by 1/2.

The math for this would look like this:

(2/3) ÷ (1/2) = (2/3) * (2/1) = (4/6)

Now, it’s hard to do computation with 4/6, as it is simplified fraction, so we can simplifying it.

(4/6) = (2/3)

So, 2/3 divided by 2 equals 2/3.

It is a bit tricky, but it is important to remember that dividing by a whole number is the same as multiplying by its reciprocal, which is a fraction with a numerator of 1.

You can also divide fractions by whole numbers using a different method called, ‘Multiply by the reciprocal’. If you want to divide 2/3 by 2, Instead of dividing, you will multiply by reciprocal of 2 which is 1/2.

2/3 * 1/2 = 1/3

So, 2/3 divided by 2 equals to 1/3

Another example:

Let’s divide 3/4 by 3. 3/4 ÷ 3 = 3/4 * (1/3) = (3/12) = (1/4)

So, 3/4 divided by 3 equals 1/4.

This is a basic introduction to dividing fractions by whole numbers. With practice, you’ll be able to do this kind of math quickly and easily. Remember to always keep the numerator and denominator in their proper places, and remember to multiply by the reciprocal of the whole number when you want to divide by it.

I hope you have a better understanding of dividing fractions by whole numbers now! Remember to practice dividing different fractions by whole numbers. Happy Learning!

Division-of-fractions-with-whole-numbers

Division of fractions with whole numbers quiz

Practice division of fractions with whole numbers math quiz. Test your skills through this.

Dividing fractions by whole numbers quiz for online practice

Interactive math practice for children online. Dividing fractions by whole numbers quiz for online practice. Children in 4th, 5th, 6th and 7th grade will find this a useful resource. This could also serve as a math game, math quiz or math test as per user. Teachers and parents can use this to supplement their fraction lessons. Improve mental math skills with out math trivia questions. Cool math game online.

Division of fractions by whole numbers can be a tricky concept for kids to understand, but with some practice and the right approach, it can be made easy. To start, let’s first define what a fraction is.

A fraction is a way to express part of a whole. It is made up of two parts: the numerator (the top number) and the denominator (the bottom number). For example, if you have a pizza and you want to share it with two friends, you can express that as a fraction. You would say, “I have half a pizza” and write it as 1/2. This means that you have one out of two equal parts of the pizza.

Now, let’s talk about division. Division is the opposite of multiplication. Instead of combining numbers, we are separating them. For example, if you have eight cookies and you want to give them to four friends, you can say, “Each friend gets two cookies” and write it as 8 ÷ 4 = 2.

When we divide a fraction by a whole number, we are still separating parts of a whole. However, instead of separating whole objects, like cookies, we are separating parts of a fraction. For example, if we have two-thirds of a pizza and we want to divide it between three friends, we can write it as 2/3 ÷ 3.

To divide a fraction by a whole number, we can use a special method called “flip and multiply.” This means we take the whole number and turn it into a fraction by putting it over 1. Then, we flip the fraction (swap the numerator and denominator) and multiply it by the original fraction.

For example, let’s go back to our 2/3 of a pizza and three friends. We want to divide 2/3 by 3. To do this, we first turn 3 into a fraction by putting it over 1, like this: 3/1. Next, we flip it by swapping the numerator and denominator, like this: 1/3. Finally, we multiply 2/3 by 1/3. This gives us:

2/3 x 1/3 = 2/3 x 1/3 = (2 x 1) / (3 x 3) = 2/9

This means that each friend gets 2/9 of a pizza.

It’s important to note that when we divide a fraction by a whole number, the result is still a fraction. However, we can also write the answer in simplest form. This means that we divide both the numerator and denominator by any common factors they have. For example, in our answer of 2/9, both the numerator and denominator can be divided by 2, which gives us:

2/9 = (2 ÷ 2) / (9 ÷ 2) = 1/4

Now, each friend gets 1/4 of a pizza.

In conclusion, division of fractions by whole numbers can be a tricky concept, but with the help of the “flip and multiply” method and writing the answer in simplest form, it can be made easy for kids to understand. With practice and a clear understanding of fractions and division, kids will be able to divide fractions by whole numbers with confidence.

Division-of-mixed-fractions

Division of mixed fractions quiz

In this quiz you will learn division of mixed fractions.

Dividing mixed fractions math quiz to test children online

Dividing mixed fractions math quiz to test children online. This is an interactive online multiple choice quiz to test math skills on fractions. Through this math game children in 3rd, 4th, 5th, 6th and 7th grade will improve their ability to solve math problems that entail division of fractions. Each problem is a MCQ in which kids have to solve the problem and drag and match corresponding answers. This game will work in a classroom and at home as a supplementary math exercise.

A mixed fraction is a combination of a whole number and a fraction. It’s written with the whole number followed by a space, and then the fraction. For example, 3 1/2 is a mixed fraction that represents three and a half.

Dividing mixed fractions can be a bit tricky, but with a little bit of practice, it’s not that difficult. Let’s start with an example:

Let’s say we want to divide 3 1/2 by 1 1/4. To do this, we first need to convert the mixed fractions into improper fractions. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number).

We can convert the mixed fraction 3 1/2 into an improper fraction by multiplying the whole number (3) by the denominator (2) and then adding the numerator (1). So 3 1/2 becomes 7/2.

Similarly we can convert 1 1/4 into an improper fraction 5/4.

Now that we have both mixed fractions as improper fractions, we can divide them just as we would with any other fractions.

So 7/2 divided by 5/4 would be (7/2) * (4/5) = 28/10 = 2 and 8/10

The final answer is 2 8/10 which can be written as 2.8 which is a mixed fraction

It’s worth noting that this is just one way to divide mixed fractions. An alternate way is to convert the mixed fraction to an improper fraction, and then dividing it as usual. But the process is the same.

Another example, suppose we want to divide 2 and 3/5 by 4 and 2/5. We can convert 2 and 3/5 into an improper fraction by multiplying the whole number by the denominator of the fraction, adding the numerator, and then add the whole number. So it becomes 23/5. Similarly, 4 and 2/5 becomes 22/5 then (23/5) / (22/5) = 23/5 * 5/22 = 23/22 = 1 and 1/22

It’s important to remember that dividing mixed fractions is not the same as dividing whole numbers. It’s important to remember to convert the mixed fractions to improper fractions before dividing them, and make sure to simplify the answer whenever possible.

You may find it helpful to practice dividing mixed fractions with different numbers.

Dividing mixed fractions can be tricky at first, but with practice, it will become easier. Remember to convert mixed fractions to improper fractions, divide, and simplify the final answer.

Also, it’s important to have a good understanding of basic operations with fractions, i.e. addition, subtraction, multiplication and division before diving into mixed fraction operation.

Find-the-percentage-of-money-values

Find the percentage of money values quiz

In this quiz you will learn how to find percentage of money values.

Finding money values involving percentages online math quiz

This exercise entails finding money values involving percentages. It is an interactive online math quiz in which children with solve problems and find answers that match. This game will improve skills for children in 3rd, 4th, 5th, 6th and 7th grades. The benefits of such quizzes is that they improve mental math abilities for kids. They will also improve kid’s ability to solve logic and word problems. Have fun online.

Percentage is a way to express a number as a fraction of 100. It’s often used to show how much of something there is in relation to the whole. In this case, we will be talking about how to find the percentage of money values.

Let’s start with an example. Imagine you have $20 and you want to find out what 10% of that is. To find the percentage of a money value, we can use a simple formula: (money value x percentage) / 100. In this case, the formula would look like this: (20 x 10) / 100 = 2. This means that 10% of $20 is $2.

Another way to find the percentage of a money value is to divide the money value by the percentage, and then multiply the answer by 100. For example, if you want to find out what 20% of $30 is, you would divide $30 by 20, and then multiply the answer by 100.

30 / 20 = 1.5 1.5 x 100 = 150

This means that 20% of $30 is $15.

It’s also possible to find the percentage of money values by using a calculator or by moving the decimal point. For example, if you want to find out what 15% of $25 is, you can move the decimal point one place to the left and multiply the answer by 15.

25 x .15 = 3.75

This means that 15% of $25 is $3.75.

Sometimes, you may also need to find the percentage of money values in order to calculate discounts or sales tax. For example, if a shirt costs $20 and is on sale for 10% off, you can use the percentage formula to find out how much money you will save.

20 x 10 / 100 = 2

This means that the shirt is $2 off, and the sale price would be $18.

In addition, when you are calculating the sales tax on a purchase, you can find the percentage of the money value by multiplying the cost of the purchase by the sales tax rate. For example, if the sales tax rate is 7% and you are buying a shirt for $20, you can calculate the sales tax by using the percentage formula.

20 x 7 / 100 = 1.4

This means that the sales tax on the shirt is $1.4.

In conclusion, knowing how to find the percentage of money values is an important concept for kids to understand, as it can be used in many different situations. By using the simple formula (money value x percentage) / 100 or by moving the decimal point, kids can easily calculate discounts, sales tax, and other money-related problems with confidence. With practice and a clear understanding of percentages, kids will be able to use this skill in their everyday life.

Finding-denominators-of-equivalent-fractions

Finding denominators of equivalent fractions quiz

Through this quiz you will learn denominators of equivalent fractions online.

Learn to find the missing denominators of equivalent fractions math quiz

In this exercise, learn to find the missing denominators of equivalent fractions. This is a math quiz with interactive online tests to take. At the end of the quiz, the score is displayed. This quiz enables instant feedback so that children can use it as a self-study aid. This also aid teachers and parents to supplement their kid’s lessons. Improve your algebra II skills by playing this online game – Math trive for 3rd, 4th, 5th, 6th and 7th grade children.

A denominator is the bottom number in a fraction. It tells us how many equal parts the whole is divided into. When we have two fractions that represent the same value, we say they are equivalent fractions.

For example, 1/2 and 2/4 are equivalent fractions, because they both represent the same amount, even though they have different numerators and denominators.

When we want to find the denominator of an equivalent fraction, there are a few ways to do it. One of the easiest ways is to use a process called “cross-multiplication.” This method involves multiplying the numerator of one fraction by the denominator of the other fraction, and vice versa.

For example, let’s say we have 1/2 and we want to find an equivalent fraction with a denominator of 6. To use cross-multiplication, we would multiply 1 (the numerator of the first fraction) by 6 (the denominator of the second fraction), and then multiply 2 (the denominator of the first fraction) by 3 (the numerator of the second fraction). This gives us 16 = 6 and 23 = 6.

Now we can set these two numbers equal to each other, 6 = 6. We have now found that the equivalent fraction of 1/2 with a denominator of 6 is 3/6 which is same as 1/2.

Another way to find an equivalent fraction with a denominator of 6, you can multiply the numerator and denominator of the original fraction (1/2) by 3. 1/2 multiplied by 3 is 3/6 which is equivalent fraction.

We can also find equivalent fractions by using the “least common multiple” (LCM) of the denominators. The least common multiple of two numbers is the smallest number that is a multiple of both numbers. In this example, the least common multiple of 2 and 6 is 6, so we can use this as the denominator for the equivalent fraction.

Another way to find the denominator of the equivalent fractions is by dividing the original denominator by the greatest common factor (GCF) of the denominator, and then multiplying it with the numerator.

For example, let’s say we have the fraction 3/4 and we want to find an equivalent fraction with a denominator of 20. To do this, we first need to find the GCF of 4 and 20, which is 4. Then we divide 20 by 4 which gives us 5. Now we multiply 3 with 5 which gives us 15. So, the equivalent fraction is 15/20.

It’s also important to note that dividing a fraction by a fraction is the same as multiplying by its reciprocal. So (3/4) / (5/20) = (3/4) * (20/5) = 3 * 4 = 12/20

It’s also important to note that changing the denominator of a fraction does not change its value. 3/4 is the same as 12/20 and 6/8, etc.

In general, it is important to have a good understanding of fractions to be able to find equivalent fractions with a given denominator. Practice and understanding the properties of fractions, like multiples and common factors, will also help.

Finding-equivalent-fractions-with-two-fractions

Finding equivalent fractions with two fractions quiz

Test your skills and practice this quiz finding equivalent fractions with two fractions.

Finding and completing equivalent fractions math quiz online

This is an interactive online math quiz on finding and completing equivalent fractions. In this exercise kids have to find missing denominators or numerators that make two fractions equivalent. This is a suitable math test for kids in 3rd, 4th, 5th and 6th grade can use both at home and in school to review their math skills. Improve pre – algebra skills as required in more advanced grades.

An equivalent fraction is a fraction that has the same value as another fraction but has a different numerator and denominator. For example, 1/2 and 2/4 are equivalent fractions because they both represent the same part of a whole (half). In this article, we will be discussing how to find the numerator of equivalent fractions.

The first step in finding the numerator of an equivalent fraction is to understand the concept of common denominators. A common denominator is a number that can be divided evenly by both the numerator and denominator of a fraction. For example, the common denominator of 1/2 and 2/4 is 4.

To find the numerator of an equivalent fraction, we can use a method called cross-multiplication. This method involves multiplying the numerator of one fraction by the denominator of the other fraction, and then multiplying the denominator of one fraction by the numerator of the other fraction. Then, we compare the two products.

For example, let’s say we have the fraction 3/4 and we want to find an equivalent fraction with a common denominator of 8. To do this, we would cross-multiply:

3 x 8 = 24 4 x 2 = 8

Since 24 and 8 are equivalent, we know that 3/4 is equivalent to 3/4 x 2/2 = 6/8.

Another way to find the numerator of an equivalent fraction is by multiplying or dividing the numerator and denominator by the same number. When we multiply or divide both the numerator and denominator by the same number, the value of the fraction stays the same.

For example, if we have the fraction 1/3 and we want to find an equivalent fraction with a denominator of 9. To do this, we can multiply both the numerator and denominator by 3:

1 x 3 = 3 3 x 3 = 9

Now, we have the equivalent fraction 3/9.

It’s important to remember that when we multiply or divide the numerator and denominator by the same number, the value of the fraction stays the same, but the numerator and denominator are different.

In conclusion, finding the numerator of an equivalent fraction is a useful skill for kids to learn, as it helps them understand the concept of fractions and how they relate to one another. By using the cross-multiplication method or by multiplying or dividing the numerator and denominator by the same number, kids can easily find the numerator of equivalent fractions with confidence. With practice and a clear understanding of fractions, kids will be able to use this skill in their everyday life and math class.