Fractions-vocabulary-and-expressions

Fractions vocabulary and expressions quiz

Practice and test your skills through Fractions vocabulary and expressions quiz

Math quiz to teach children vocabulary related to fractions

Math quiz to teach children vocabulary related to fractions. It is important for children to understand how to express fractions in words and vice-versa. Children should also understand concepts like denominator and numerator, multiples and factors. All these notions are essential for teaching topics related to fractions. It is therefore important to build a base for children in 1st, 2nd and 3rd grades to build on. This is an interactive multiple choice questions quiz.

Fractions are a way to represent a part of a whole or a part of a group. They are usually written as a number or letter over another number or letter, with a line separating the two. For example, “1/2” is read as “one-half,” “2/3” is read as “two-thirds,” and “3/4” is read as “three-fourths.”

There are several basic vocabulary words and expressions that are commonly used when talking about fractions:

  • Numerator: The top number or letter in a fraction. For example, in the fraction “1/2,” the numerator is “1.”
  • Denominator: The bottom number or letter in a fraction. For example, in the fraction “1/2,” the denominator is “2.”
  • Fraction bar: The line separating the numerator and denominator in a fraction.
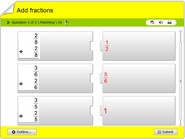
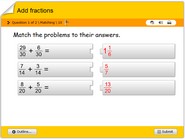
  • Simplify: To rewrite a fraction in its simplest form. For example, “6/8” can be simplified to “3/4.”
  • Equivalent fractions: Fractions that represent the same value, even though they may look different. For example, “1/2” and “2/4” are equivalent fractions because they both represent the same value (half).
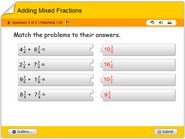
  • Mixed number: A number that is made up of a whole number and a fraction. For example, “2 1/2” is a mixed number.
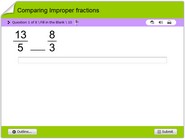
  • Improper fraction: A fraction where the numerator is larger than the denominator. For example, “7/4” is an improper fraction.
  • Proper fraction: A fraction where the numerator is smaller than the denominator. For example, “1/2” is a proper fraction.
  • Unit fraction: A fraction where the numerator is 1 and the denominator is a positive integer. For example, “1/2” is a unit fraction.

Now, let’s take a look at some common fractions and their corresponding vocabulary words and expressions:

  • Half: “1/2” is called “half.”
  • Third: “1/3” is called “one-third” or simply “a third.”
  • Quarter: “1/4” is called “one-quarter” or simply “a quarter.”
  • Fifth: “1/5” is called “one-fifth” or simply “a fifth.”
  • Sixth: “1/6” is called “one-sixth” or simply “a sixth.”
  • Seventh: “1/7” is called “one-seventh” or simply “a seventh.”
  • Eighth: “1/8” is called “one-eighth” or simply “an eighth.”
  • Ninth: “1/9” is called “one-ninth” or simply “a ninth.”
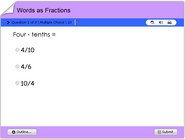
  • Tenth: “1/10” is called “one-tenth” or simply “a tenth.”

Here are some examples of how these fractions and expressions can be used in sentences:

  • “I need half a cup of sugar for this recipe.”
  • “There are two thirds of a mile left until we reach our destination.”
  • “I’m going to cut this pizza into quarters so that we can share it.”
  • “There are five fifths in a whole.”
  • “I’m going to divide this pie into sixths and save some for later.”
  • “There are seven sevenths in a week.”
  • “I’m going to pay you an eighth of the total cost.”
Identifying-fractions

Identifying fractions quiz

Identifying fractions quiz exercise for math practice online.

Identify fractions from pictures interactive math quiz online.

This is an interactive math quiz online in which children have to identify fraction values from looking at shaded portions of a shape or picture. This is a great way to introduce kids to the notion of fractions. This is sort of a multiple choice questions trivia exercise on fractions which children in 1st, 2nd, 3rd and 4th grades can use to review and practice online. This is also a cool math exercise since it is meant to enable children to self- test their skills. At the end of the exercise children will figure out their test score and also get instant feedback as they play.

Identifying fractions with pictures can be a fun and engaging way for students to learn about this important mathematical concept. Fractions represent a part of a whole, and understanding them is crucial for performing a variety of mathematical operations.

One way to introduce fractions using pictures is to start with concrete examples. For example, you could show students a picture of a pie and ask them to identify the fraction that represents a specific slice. You could also use pictures of objects that can be easily divided into equal parts, such as a pizza or a bar of chocolate.

Another approach is to use visual models to represent fractions. One common visual model is the number line, which can be used to represent fractions as points along a line. For example, a fraction such as 1/2 can be represented by a point halfway along the number line.

Another visual model is the fraction circle, which is a circle divided into equal parts. Each part can be labeled with a fraction, such as 1/4 or 3/8. This model is particularly useful for showing students how fractions can be simplified or reduced to their lowest terms.

It’s also important for students to understand the relationship between fractions and decimals. This can be demonstrated using a visual model such as the hundredths grid, which is a grid made up of 100 equal squares. Each square can be labeled with a decimal equivalent of a fraction, such as 0.25 for 1/4 or 0.75 for 3/4.

In addition to using visual models, there are several other strategies that can be used to help students identify fractions with pictures. For example, you could use manipulatives such as fraction strips or tiles to physically model fractions and help students understand the concept of a part of a whole.

Another strategy is to use games and activities to reinforce learning. For example, you could create a scavenger hunt where students have to find and identify fractions in pictures around the classroom. You could also use online resources and apps to provide additional practice and support for students as they learn about fractions.

It’s also important to provide students with plenty of opportunities to practice identifying fractions with pictures. This can be done through worksheets, quizzes, and other forms of assessment. As students become more comfortable with the concept, you can gradually increase the level of difficulty to help them continue to grow and develop their skills.

Overall, identifying fractions with pictures can be a fun and effective way to teach this important mathematical concept. By using visual models and other strategies, students can gain a deeper understanding of fractions and be better equipped to perform a variety of mathematical operations.

Probability-with-fractions

Probability with fractions quiz

 Probability with fractions quiz, Test your skills through this exercise

Finding the probability with notions of fractions, math quiz online

The probability of something happening or not is is common in daily life phenomena. We often talk to the likelihood or unlikelihood of something happening. For example if you spin the wheel what will happen etc. The notion of fractions is also part of this concept and in this interactive math online quiz children will solve problems that involve probability. This is a multiple choice test and it is a great way for kids to get extra practice at home or in the classroom. This quiz is also in line with common core state standards for 5th, 6th and 7th grades.

Probability is a measure of the likelihood of an event occurring. It is expressed as a fraction, with the numerator representing the number of successful outcomes and the denominator representing the total number of possible outcomes. For example, if you were flipping a coin, the probability of getting heads would be 1/2, since there are two possible outcomes (heads or tails) and only one of them is a successful outcome (getting heads).

Probability can also be expressed as a percentage. To convert a probability from fraction form to percentage form, simply multiply the fraction by 100%. For example, the probability of getting heads when flipping a coin is 1/2, or 50% in percentage form.

There are several rules that hold true for probability. The first is that the probability of an event occurring is always between 0 and 1 (or 0% and 100% in percentage form). An event with a probability of 0 means that it is impossible for the event to occur, while an event with a probability of 1 (or 100%) means that it is certain to occur.

The second rule is the sum rule, which states that the probability of all possible outcomes occurring is always equal to 1 (or 100%). For example, the probability of flipping heads or tails when flipping a coin is 1, since both outcomes are possible.

The third rule is the multiplication rule, which states that the probability of two events occurring is equal to the probability of the first event occurring multiplied by the probability of the second event occurring. For example, if you have a bag with 5 red balls and 5 blue balls, and you draw one ball out of the bag without replacing it, the probability of drawing a red ball and then a blue ball would be (5/10) * (4/9) = 2/9.

Probability can be used to make predictions about the likelihood of an event occurring. For example, if you know that it rains on 20% of the days in a particular month, you can use this information to predict the probability of it raining on a given day in that month.

Probability can also be used to make decisions. For example, if you are deciding whether or not to buy a lottery ticket, you might consider the probability of winning the lottery as part of your decision-making process.

There are many different types of probability, including classical probability, empirical probability, and subjective probability. Classical probability is based on the idea that all outcomes are equally likely to occur, while empirical probability is based on observations of events that have already occurred. Subjective probability is based on an individual’s personal belief about the likelihood of an event occurring.

Probability theory is a branch of mathematics that deals with the study of probability. It has many applications in fields such as finance, insurance, and statistics. Probability is a fundamental concept in mathematics and has many practical applications in real-world situations.

Add-fractions-horizontal-arrangement

Add fractions horizontal arrangement quiz

Learn to add fractions in a horizontal arrangement,  math quiz online.

Addition of fractions math test online for children

Addition of fractions math test online for children in 3rd to 7th grades. To successfully take this quiz, children must understand notions of finding the LCM of two numbers. They also have to understand the rules needed in adding fractions. This quiz will improve mental math abilities of children. It will also enable them to self-evaluate their math skills and improve on areas of weakness. This quiz is multiple choice math trivia online and there is no limit as to how many times it could be taken.

When we add fractions, we are finding the total amount when we combine two or more parts together. Imagine you have a pizza and you want to divide it into 4 equal slices. Each slice would be one fourth of the pizza, or 1/4. If you had two slices, the total amount of pizza you would have would be 2/4, which is the same as 1/2. This is because when you add the two parts together (2/4), you are finding the whole (1/2).

When adding fractions, it is important to make sure that the fractions have the same denominator, or bottom number. This is because the denominator tells us how many parts the whole is divided into. If the denominators are different, it can be difficult to add the fractions because they are not talking about the same number of parts.

For example, if you wanted to add 1/4 and 1/3 together, you would need to first find a common denominator. A common denominator is a number that both fractions can be converted to, so that they have the same denominator. In this case, a common denominator would be 12 because 4 and 12 have no common factors other than 1 and 3 and 12 are the least common multiple.

Now that we have a common denominator, we can convert 1/4 to 3/12 and 1/3 to 4/12. Now we can add these fractions, 3/12 + 4/12 = 7/12

It is also possible to add fractions that are arranged horizontally, which means the fractions are lined up next to each other. When adding fractions in this way, it is important to remember that the denominators, or bottom numbers, must still be the same.

For example, if you wanted to add 2/5, 3/5 and 1/5 together, you would line them up horizontally and add the numerators, or top numbers, together:

2/5 + 3/5 + 1/5 = 6/5

It is important to notice in this case, the result of this sum is a mixed number. 6/5 is the same as 1 1/5, which is the same as 6/5.

It’s very important to note that when working with fractions, it is important to simplify the fractions to lowest terms whenever possible.

In general, when adding fractions, you can think of it as combining parts of a whole. The denominators tell us how many parts the whole is divided into, and the numerators tell us how many of those parts we have. By adding the numerators together and keeping the denominator the same, we can find the total amount when we combine the parts together.

In summary, when adding fractions, it’s necessary to have the denominators the same and add the numerators together. In case the denominators are not the same, it’s required to find a common denominator first. Also, it’s always a good idea to simplify the fractions to lowest terms whenever possible.

Addition-of-fractions-vertically-arranged

Addition of fractions vertically arranged quiz

Addition of fractions vertically arranged exercise test your skills.

Interactive math game on adding fractions, 3rd to 7th grade math

This is an interactive math game on adding fractions for kids in 3rd, 4th, 5th, 6th and 7th grades. This takes the form of a multiple choice questions quiz online which kids can use to check their skills on fraction. This is also a drag and drop activity for children at different levels. To the right are the problems and to the left the answers. simply solve the problem and then drag and drop the correct answer that corresponds. At the end of each game, children will get their scores displayed. This is a flexible way to self-evaluate yourself.

When we add fractions, we are finding the total value of two or more parts. In order to add fractions, the denominators (the bottom numbers) of the fractions must be the same. If the denominators are not the same, we must find a common denominator before we can add the fractions.

One way to add fractions is by using a method called “vertical addition.” In this method, we write the fractions one above the other, with the numerators (the top numbers) lined up, and the denominators lined up below them. We then add the numerators together, and keep the denominator the same.

For example, let’s say we want to add the fractions 1/4 and 1/4. We write them vertically, with the numerators lined up and the denominators lined up below:

1/4
+1/4
-----

Now we add the numerators, which in this case are both 1. We get:

1/4
+1/4
-----
2/4

We now have the sum of the two fractions which is 2/4. We can simplify this by dividing the numerator and denominator by a common factor of 2, to get the simplified fraction 1/2. So the sum of 1/4 and 1/4 is 1/2.

This method of adding fractions can be used for adding more than two fractions, just keep adding the numerators and keep the denominator same.

1/4
+1/4
+1/4
-----
3/4

As we can see that when we added 1/4 + 1/4 + 1/4 we get 3/4.

It’s also very important to note that the fractions need to be written with the same denominator, and that denominator will be the least common multiple(LCM) of all the fractions, For example:

2/3
+3/5
-----

The LCM for the above fractions is 15. So the fractions will be written as:

10/15
+9/15
-----
19/15

Adding fractions can be a bit tricky at first, but with practice and understanding, it becomes easy and fun. It’s also important to understand when to simplify the fraction like we did in 2/4 to 1/2.

When adding or subtracting fractions, it’s important to remember to find a common denominator first, if the denominators are not the same. And always simplify the fraction if possible.

In addition to vertical addition, there are other ways to add fractions, such as finding a common denominator and then adding or subtracting the numerators, or by using a method called “cross-multiplication.” But vertical addition is a useful and straightforward method that students can use to add fractions.

Addition-of-fractions-with-large-denominators

Addition of fractions with large denominators quiz

Learn how to do Addition of fractions with large denominators through this online quiz

 

Math quiz involving addition of fractions with large denominators

Math quiz involving addition of fractions with large denominators for children in 4th, 5th, 6th and 7th grades. This is an interactive online math test which kids can use to test their skills after school. In each exercise, children have to solve an addition problem and find the corresponding answer. After doing this, players should drag and match to appropriate locations. This quiz could also be used as a math game or as a multiple choice question trivia. Learn math with fun.

When we add fractions, we’re finding the total amount when we combine two or more parts together. One way we can add fractions is by making sure that the denominators, or bottom numbers, are the same.

However, sometimes the denominators can be very large numbers, making it difficult to add the fractions together. In these cases, we can use a method called “finding a common denominator” to help us add the fractions.

A common denominator is a number that both fractions can be converted to, so that they have the same denominator. To find a common denominator for two fractions, we can use the least common multiple (LCM) of the denominators. The least common multiple is the smallest number that both denominators can divide into without leaving a remainder.

For example, let’s say we want to add the fractions 2/15 and 3/20. To find a common denominator, we can use the least common multiple of 15 and 20. The least common multiple of 15 and 20 is 60. This means that we can convert 2/15 to 8/60 and 3/20 to 9/60, so that both fractions have the same denominator of 60.

Now that we have a common denominator, we can add the fractions together: 8/60 + 9/60 = 17/60

In this case, 17/60 is a simplified fraction, we can use the greatest common factor (GCF) to simplify more. The GCF of 17 and 60 is 1.

Another way of achieving the same result is by multiplying the numerator and denominator of the first fraction by the same value, and then doing the same for the second fraction.

For example, you could multiply the numerator and denominator of the first fraction by 4 and the numerator and denominator of the second fraction by 3, this way: (2/15) * (4/4) = 8/60 and (3/20) * (3/3) = 9/60, then add them 8/60 + 9/60 = 17/60

It’s important to note that when working with fractions with large denominators, it is important to simplify the fractions to lowest terms whenever possible, as we showed in the previous example.

Another example let’s say we have to add 2/45 + 5/90, to add them we need to find a common denominator. We can use the LCM of 45 and 90, which is 90. Then we convert the fractions into 9/90 and 5/90, which we can add them together to get 14/90

It’s important to note that sometimes, finding a common denominator for fractions with large denominators can be a bit more difficult and time consuming, but by breaking it down and following these steps, it can be a manageable task.

In summary, when adding fractions with large denominators, it’s necessary to find a common denominator. The least common multiple of the denominators is usually the common denominator. To convert the fractions, we can multiply both the numerator and denominator by the same value. And remember it’s always a good idea to simplify the fractions to lowest terms whenever possible.

Addition-of-mixed-fractions

Addition of mixed fractions quiz

Practice Addition of mixed fractions math online quiz.

Adding mixed-fractions interactive online test

Adding mixed-fractions interactive online test for children in 4th, 5th, 6th and 7th grades. This is a multiple choice trivia involving drag and drop exercises. Children will improve their math skills through this test. At the end of the quiz a score will be displayed. This is an online practice activity but we also offer the option of downloading worksheets and reviewing while at home. This math quiz could also serve as a cool math game which kids can use both at home and in the classroom.

When we add mixed fractions, we are finding the total value of two or more mixed numbers. A mixed number is a whole number and a fraction combined. For example, 2 1/2 is a mixed number because it is made up of the whole number 2 and the fraction 1/2.

To add mixed fractions, we start by adding the whole numbers together. So in example: 2 3/5 + 3 2/5, First we will add 2 + 3 which equals to 5.

Next, we add the fractions separately, just like we do when adding regular fractions. In the example, 3/5 + 2/5. Since the denominators are the same (5), we can simply add the numerators (the top numbers of the fractions), which gives us 3/5 + 2/5 = 5/5 = 1.

Now, we add the sum of the whole numbers (5) to the sum of the fractions (1) to get the final answer, which is 5 + 1 = 6 1/5. So, the sum of 2 3/5 and 3 2/5 is 6 1/5.

It’s also very important to note that to add mixed fractions, the fractions should have the same denominator. In case they don’t, we need to find the least common denominator (LCD) and change the fraction to have the same denominator before adding them.

Comparing-fractions

Comparing fractions quiz

Test your skills with this online exercise Comparing fractions quiz.

Comparison of two fractions quiz online, greater, less than or equal to

Comparison of two fractions quiz online, greater, less than or equal to. This quiz will also serve as a math game for children. This activity is in line with the curriculum for 3rd, 4th, 5th and 6th grades, hence will serve as a review exercise for children at this level. It is also a free math activity which teachers and parents could use to supplement their math course. After taking this quiz, print out math worksheets on the same topic and get more practice offline.

When we compare fractions, we are looking at two or more fractions and determining which one is larger or smaller. To compare fractions, we need to make sure that the fractions have the same denominator, or bottom number. This is because the denominator tells us how many parts the whole is divided into, and if the denominators are different, it can be difficult to compare the fractions because they are not talking about the same number of parts.

For example, if you wanted to compare the fractions 1/4 and 1/3, you would need to first find a common denominator. A common denominator is a number that both fractions can be converted to, so that they have the same denominator. In this case, a common denominator would be 12 because 4 and 12 have no common factors other than 1 and 3 and 12 is the least common multiple. Now that we have a common denominator, we can convert 1/4 to 3/12 and 1/3 to 4/12. Now we can compare these fractions.

3/12 < 4/12

We can tell that 1/3 is greater than 1/4 because 4 is larger than 3.

Another way to compare fractions is by looking at the numerator, or top number. The numerator tells us how many parts of the whole we have. In general, the larger the numerator, the larger the fraction.

For example, if you wanted to compare the fractions 2/5 and 3/5, you would look at the numerators.

2/5 < 3/5

We can tell that 3/5 is greater than 2/5 because 3 is greater than 2.

We can also convert the fractions to decimal numbers, by dividing the numerator by the denominator, that way is much easier to compare them.

Another example, let’s say we have to compare the fractions 5/8 and 7/12, we can convert them to decimals, 5/8 = .625 and 7/12 = .583, this way we can tell that 5/8 is greater than 7/12

It’s important to notice that when we are comparing fractions with different denominators it’s necessary to have a common denominator, or convert them into decimal numbers, to have a fair comparison.

Another way of comparing fractions is by simplifying them. When a fraction is simplified, it means that the numerator and denominator have no common factors other than 1. Simplifying a fraction makes it easier to compare because it shows the fraction in its simplest form.

For example, let’s compare the fractions 6/12 and 8/16, in order to compare them, we can simplify them first, 6/12 can be simplified to 3/6, which is the same as 1/2, and 8/16 can be simplified to 1/2

1/2 = 1/2

We can tell that both fractions are equal, 6/12 and 8/16 are the same.

In summary, when comparing fractions, it’s necessary to make sure that the fractions have the same denominator, or convert them into decimal numbers, to have a fair comparison. Another way of comparing them is by looking at the numerator, the larger the numerator, the larger the fraction. Also, it’s a good idea to simplify the fractions whenever possible.

Comparing-improper-fractions

Comparing improper fractions quiz

Learn Comparing improper fractions exercise. Online math practice check your skills.

Learn how to compare improper fractions in an online quiz game

Learn how to compare improper fractions in an online quiz game. Improper fractions have numerators that are larger than their denominators. A good way of comparing them is to first reduce them to their lowest terms. This math activity is a good test for children in 4th, 5th, 6th and 7th grades. Comparison of fractions also entail using phrases like less than, greater than and equal to. Learn how to use this vocabulary in real problems. Cool math quiz online for children.

When we compare improper fractions, we are determining which one is greater or smaller than the other. An improper fraction is a fraction where the numerator (the top number) is larger than the denominator (the bottom number).

To compare improper fractions, we have a few methods, one of them is by looking at the numerators (the top numbers) and comparing them. If the numerator of one fraction is larger than the numerator of the other fraction, then the first fraction is larger. for example, 5/3 is larger than 4/3 because 5 is greater than 4.

Another way is by converting them to mixed numbers and then comparing the whole numbers. To convert an improper fraction to a mixed number, we divide the numerator by the denominator and add the remainder as a whole number. For example: 7/4 is smaller than 9/5, because when we convert 7/4 to a mixed number it will be 1 3/4 and 9/5 will be 1 4/5. 1 4/5 is bigger than 1 3/4

Another way is by cross-multiplying the fractions. This method compares the products of the numerators and denominators. For example: 7/4 is smaller than 9/5 because when we cross-multiply we get 35/4 and 36/5. and 36/5 is greater than 35/4

It’s also very important to simplify the fractions if they can be simplified before comparing them.

In conclusion, comparing improper fractions can be done by comparing the numerators, converting them to mixed numbers, or cross-multiplying them. The most important thing to remember is that the fractions need to have the same denominator to be able to compare them directly. It’s also a good idea to practice comparing different improper fractions to become comfortable and confident with the process.

Comparing-mixed-fractions

Comparing mixed fractions quiz

In Comparing mixed fractions exercise you will learn how to compare mixed fractions in easy way?

Math quiz online for children to learn how to compare mixed fractions

This is an interactive online math quiz to test kids skills on how to compare mixed fractions. In this quiz, children will solve the problem, fill in the correct answer and submit. This quiz can be taken by children in 3rd, 4th, 5th, 6th and 7th grade who need to test and review their skills. This math quiz could also be perceived as a cool math game suitable for classroom and homeschool use. Have fun online and also learn the notion of comparing mixed fractions.

A mixed fraction, also known as a mixed number, is a whole number combined with a fraction. For example, the mixed fraction 3 1/2 is equal to the whole number 3 plus the fraction 1/2.

Comparing mixed fractions can be a little tricky, but with a few simple steps, it’s easy to do. To compare mixed fractions, you first need to convert them to improper fractions. An improper fraction is a fraction where the numerator (the top number) is larger than the denominator (the bottom number). For example, the mixed fraction 3 1/2 is equal to the improper fraction 7/2.

Once the mixed fractions have been converted to improper fractions, you can use the same method for comparing fractions to compare the mixed fractions. To compare fractions, you compare the numerators (the top numbers) and the denominators (the bottom numbers) separately.

For example, let’s say we want to compare the mixed fractions 2 3/4 and 3 1/2. First, we convert them to improper fractions: 2 3/4 = 11/4 and 3 1/2 = 7/2. Then we compare the numerators: 11 is greater than 7, so we know that 2 3/4 is greater than 3 1/2.

Another method is to convert them to decimals, since it’s very easy to compare decimal numbers.

For example, Let’s compare 3 1/4 and 1 5/6. 3 1/4 = 3+1/4 = 3.25 1 5/6 = 1+5/6 = 1.83333 It is obvious that 3.25 is greater than 1.83333

It’s important to remember that when comparing mixed fractions, you need to make sure that the fractions are in their simplest form (also known as “reduced”) before comparing them. Also, converting to decimals is very useful method when it comes to compare mixed fractions, but you should be careful when converting as it might introduce inaccuracies due to lack of precision with some fractions.

By following these simple steps, you’ll be able to compare mixed fractions with ease and confidence!