Adding fractions from parts quiz
Adding fractions from parts math quiz for practice and testing your skills.
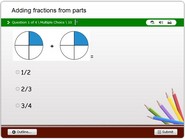
Illustrated math exercise on adding parts of fractions
Illustrated math exercise on adding parts of fractions. In this exercise, children will learn how to add portions of a shape to arrive at sums of other fractions. This is a multiple choice test questions and a trivia math quiz for children in 2nd, 3rd, 4th and 5th grades. It could serve as a math test online or a review activity at home. Each problem contains a graphic showing two fraction values shaded on a circle or any other geometric shape. Takers of the quiz have to find out the sum of both fractions with the aid of each given picture. This game also serves as an interactive online math multiple choice question test.
Adding fractions with the same denominator is a straightforward process. The sum of the fractions is equal to the sum of the numerators, with the denominator remaining the same. For example, if we have the fractions 1/2 and 1/2, we can find the sum by adding the numerators together to get 2/2, or simply 1.
However, things can get a bit more complicated when the fractions have different denominators. In this case, we need to first find a common denominator before we can add the fractions. A common denominator is a number that is a multiple of both of the fractions’ denominators.
For example, consider the fractions 1/2 and 1/3. To add these fractions, we need to find a common denominator that is a multiple of both 2 and 3. The least common multiple of 2 and 3 is 6, so we can use 6 as the common denominator.
To express 1/2 and 1/3 with a denominator of 6, we need to rewrite them as fractions with 6 as the denominator. To do this, we use the following formula:
New fraction = (numerator x common denominator) / original denominator
Using this formula, we can rewrite 1/2 as follows:
New fraction = (1 x 6) / 2 = 3/6
We can do the same thing with 1/3 to get a new fraction of 2/6.
Now that both fractions have a common denominator of 6, we can add them together by simply adding the numerators. The sum of 3/6 and 2/6 is 5/6.
Another way to add fractions with different denominators is to use the least common multiple (LCM) of the denominators as the common denominator. The LCM is the smallest number that is a multiple of both denominators. In the example above, the LCM of 2 and 3 is 6, so we could also use the LCM method to find the common denominator.
It’s important to note that the LCM is not always the same as the common denominator. For example, the fractions 1/4 and 1/6 have a common denominator of 12, but the LCM of 4 and 6 is 12. In this case, using the LCM as the common denominator would work, but it’s not always the case.
Once you have found the common denominator, the process of adding the fractions is the same as if the fractions had the same denominator. Simply add the numerators and write the sum as a fraction with the common denominator.
In summary, to add fractions with different denominators:
- Find a common denominator, either by using a multiple of both denominators or the least common multiple of the denominators.
- Rewrite each fraction with the common denominator using the formula: (numerator x common denominator) / original denominator.
- Add the numerators of the new fractions to find the sum.